Så fungerar matematiken bakom en equalizer

Låt säga att vi är givna följande ljudfil, och blir tillsagda med en pistol mot huvudet att ta bort alla frekvenser under 10 kHz.

Lätt som en plätt så klart, vi stoppar in filen i vår favorit-DAW och ”eq:ar”. Vad sa du? Ska vi göra det FÖR HAND?!

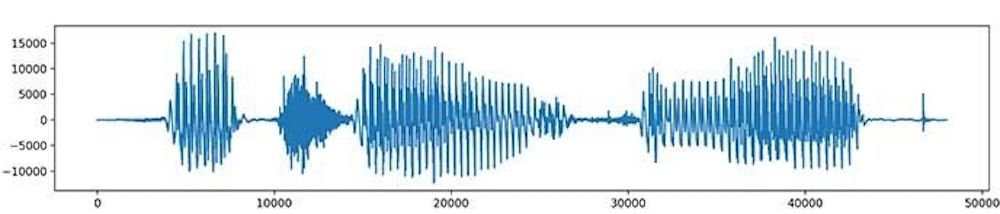
Var ska man ens börja? För det första, vad är låga frekvenser, och var hittar man dem? Allt man ser på vågformen är ju en enda röra. Sen kommer vi ihåg Fourier-transformen, och vi inser att vi kommer att klara det. Tack Gud för matematiken. Låt oss nu försöka ta oss igenom, på enklast möjliga sätt, hur en dator gör när vi ”eq:ar”.

Komplexa tal och den riktiga världen
Den som är nyfiken på matematik eller fysik kanske kommer ihåg att en lärare någon gång berättat om talet i , roten ur minus ett – det vill säga ett tal som gånger sig självt blir -1. Som du kanske känner till så är vilket ”vanligt” tal, eller reellt tal som det heter, som helst gånger sig själv alltid ett positivt tal, och därför bör man ta på sig skeptiska glasögon när vi påstår att det finns något som heter i och att i gånger i är -1. Men om vi får be om ett ”leap of faith”, så tro oss när vi säger att vi kan bygga ett talsystem där i är en av byggstenarna. Detta talsystem kallas för ”komplexa tal”, eller ibland ”imaginära tal”.

Efter att ha fått detta presenterat för sig frågar sig den skeptiska personen alltid samma sak: Hur kan man någonsin använda detta i den riktiga världen? Det ska vi svara på nu.

Att omvandla till frekvenser
En digital ljudfil är inget annat än en lista med tal som beskriver hur lufttrycket varierar över en viss tid. Det vill säga, en ljudfil kan skrivas ner så här:

A=(a(1), a(2), a(3), ..., a(N))

Där står storleken på talet a(n) för hur stark signalen är vid tiden n. Ljudfilen i bilden ovan är en lista med knappt 50 000 tal varierande mellan cirka -10 000 och 15 000.

Redan på 1800-talet, ett bra tag innan mikrofonen uppfunnits, kom en man vid namn Joseph Fourier på hur man delar upp en signal i frekvens-komponenter. Det betyder att han kunde omvandla listan A till en lista där talen beskriver hur ljudet beter sig i frekvens-domänen.

 = (â(1), â(2), â(3), ..., â(N))

Det vill säga, om â(1) har ett stort värde, då är frekvens nummer 1 stark. ”Frekvens nummer 1” har såklart ett Hz-värde, men det behöver vi inte gå in på närmare just nu. Om talet â(10) är lika med noll, då finns det ingen frekvens nummer 10 i ljudsnutten.

För den som vågar titta ser formeln för den så kallade m:te frekvens-komponenten ut såhär:

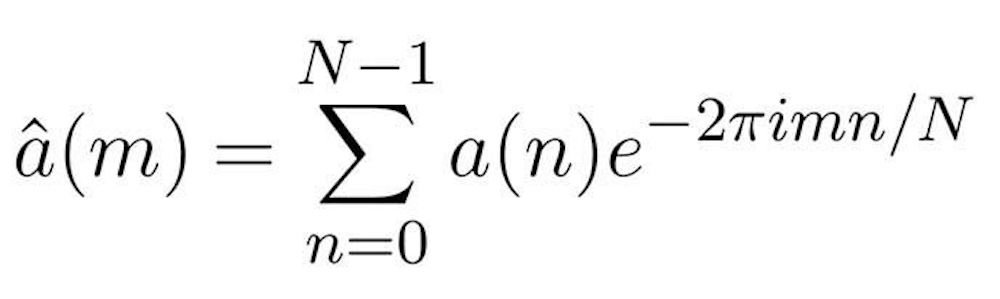
Ser ni? Förutom talet i ser vi även pi där, för att inte tala om e. Alla fundamentala matematiska konstanter som strålar samman i en formel som vi, eller i alla fall våra datorer, använder dagligen. Omvandlingen beskriven ovan kallas för Fourier-transformen av A.

Nu har vi receptet för att ta bort eller ändra styrkan på frekvenser:

1. Ta listan A som beskriver ljudsignalen och omvandla den till  i frekvens-domänen med hjälp av Fourier-transformen.
2. Leta reda på värdet â(n) som motsvarar frekvensen du vill ändra/ta bort.
3. Justera â(n).
4. Omvandla tillbaka till tidsdomänen med hjälp av den omvända Fourier-transformen.

Voila, så har vi ”eq:at”.